| 1.因式分解的3种基本方法。 2.常用因式分解公式。 3.十字相乘法及推广。 请同学们回顾前一节内容,回答以下问题 上节课我们说到因式分解在高中的很多领域比如函数变换,解析几何中的代数式变形,不等式的证明等等都有应用,可是初中阶段介绍的几种方法有一定局限性。今天我们就因式分解的方法作进一步的探讨。 1.分组分解法的基本原理: 请先看一个多项式的分解因式: 。这个题目结构非常清楚,有公因式 。这个题目结构非常清楚,有公因式 ,所以直接提取即可。但如果待分解因式的多项式是 ,所以直接提取即可。但如果待分解因式的多项式是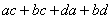 ,就不能直接提取公因式了,原因是把待分解的多项式由 ,就不能直接提取公因式了,原因是把待分解的多项式由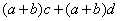 变形为比这个更原始的结构 变形为比这个更原始的结构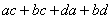 ,但我们知道两个式子是恒等的。这种情况下,分解因式的过程自然就是: ,但我们知道两个式子是恒等的。这种情况下,分解因式的过程自然就是: 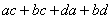 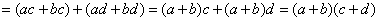 。这样分解因式的方法叫做分组分解法,即将多项式适当分组后经过局部分解,化成可以整体分解的结构,最终可以整体分解的方法。 。这样分解因式的方法叫做分组分解法,即将多项式适当分组后经过局部分解,化成可以整体分解的结构,最终可以整体分解的方法。
例1:分解因式:(1)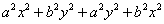 (2) (2)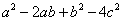 (1)分析:在多项式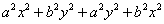 中,第一项和第三项有公因式 中,第一项和第三项有公因式 ,而第二项和第四项也有公因式 ,而第二项和第四项也有公因式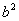 ,这样观察到局部有公因式可提取,即可完成分组这个关键步骤。 ,这样观察到局部有公因式可提取,即可完成分组这个关键步骤。 (1)解: 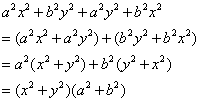
评注:这个多项式分组的方式并不唯一,也可以第一项与第四项组合,他们的本质实际都是一样的。 (2)分析:在多项式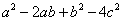 中,前三项是完全平方式,而第四项除了负号也是完全平方形式,这样前三项分成一组,最后一项分成另一组就可以构造平方差的结构。 中,前三项是完全平方式,而第四项除了负号也是完全平方形式,这样前三项分成一组,最后一项分成另一组就可以构造平方差的结构。 (2)解: 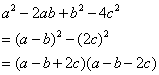
评注:这个多项式的分解因式中,其他分组的方式是不能进行分解因式的,比如前两项组合在一起,后两项组合在一起,虽然都能局部分解,但不能进行整体分解,所以这种分组的方式是失败的。在对多项式的结构没有观察清楚的前提下,分组失败是经常出现的,但只要注意分组的方向,即恒等变形过程中,化成能够在局部分解的前提下,又能整体分解的结构,就能达到分解因式的目的。分组的目的将多项式转化成可以用前三种分解的形式。 补充练习: (1) (2) (2) (3) (3) 例2分解因式: 分析:根据多项式的结构特点,经过分组和局部分解将它化成关于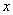 的二次三项的结构(或广义的十字相乘的结构),然后运用十字相乘法。 的二次三项的结构(或广义的十字相乘的结构),然后运用十字相乘法。 解法一: 
解法二 : 
解法三:  令 令

所以由, , , 这种方法叫做待定系数法,也在分组之后,继续分解的一种途径。待定系数应用很广泛,无论初中还是高中,这解决很多数学问题的一种方法。初中时我们强调一题多解,可是高中后,我们很多时候需要多题一解,强调通法。 其中,解法一的十字相乘是: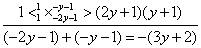 ; ; 解法二的十字相乘是: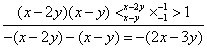 评注:本题除了上述两种方法之外,只要是经过分组和局部分解把多项式化成二次三项的形式,都能利用十字相乘法分解因式。比如:经过分组和局部分解化成关于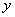 的二次三项式的结构 的二次三项式的结构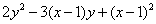 。 。 补充练习: (1) (2) 解:令 则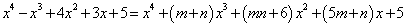 , , 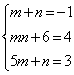 ,所以 ,所以 所以, 所以,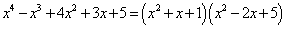
例3分解因式:(1)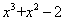 (2) (2)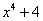 (1)分析:可以把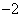 拆分成两个 拆分成两个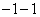 ,即 ,即 ,再分组即可,也可以添加一项变为 ,再分组即可,也可以添加一项变为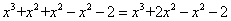 ,再分组即可,所以添项与拆项两种方法的本质是一样的。 ,再分组即可,所以添项与拆项两种方法的本质是一样的。 解一: 解二: 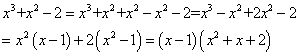
(2)分析:这个多项式不能直接运用上面所介绍的四种方法分解因式,原因是不属于三种方法的任何一种结构形式。但由于将这个多项式可以看做关于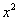 的二次式:即 的二次式:即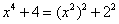 ,则容易想到配方成: ,则容易想到配方成: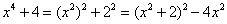 ,这样就可以分解因式。 ,这样就可以分解因式。 解: 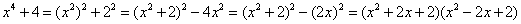
评注:另一个角度看,实际是将合并后的多项式还原成原来的结构: 即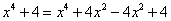 ,这样的过程我们可以说成是“填项或拆项分组法”,是“间接分组分解法”的一种。初中阶段,我们更多的是“合并”同类项,但实际数学变形当中,“拆同类项”也是非常重要的,而且不同的是:“合并”的结果是唯一的,但“拆”的形式是无穷多种(如: ,这样的过程我们可以说成是“填项或拆项分组法”,是“间接分组分解法”的一种。初中阶段,我们更多的是“合并”同类项,但实际数学变形当中,“拆同类项”也是非常重要的,而且不同的是:“合并”的结果是唯一的,但“拆”的形式是无穷多种(如: ),所以“拆”的时候要根据我们需要的结构“拆”得准才可以,无论添拆目的都是将多项式转化为可以分组分解的。 ),所以“拆”的时候要根据我们需要的结构“拆”得准才可以,无论添拆目的都是将多项式转化为可以分组分解的。 除了“填项或拆项分组法”这种“间接分组分解法”以外,有的多项式首先化简才能分组,这种分解因式的方法也属于“间接分组分解法”,这种方法就叫做“化简分组法”。比如:多项式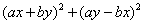 的分解因式问题。 的分解因式问题。 。 3.因式分解方法的系统归类 综上所述,整个高中阶段的分解因式需要我们掌握的方法可归类为: 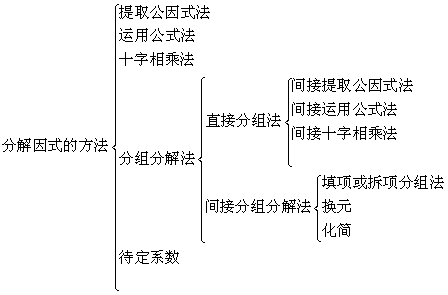
注意: 1.因式分解的方法多样性是由多项式结构的多样性引起的,即针对不同结构的多项式,采用不同的方法分解因式,所以如何选择恰当的方法关键是观察多项式的结构特征。观察的的顺序为:看是否有公因式 看是否公式结构 看是否公式结构 看是否二次三项式 看是否二次三项式 看是否可分组,以上都行不同就可考虑利用间接分组分解法。 看是否可分组,以上都行不同就可考虑利用间接分组分解法。 2.以上所提到的方法之间也是相互联系的,比如:公式法能分解的大都可用十字相乘法,十字相乘法能分解的可用分组拆项的方法转化为可提取公因式的结构等等。 3. 除了分组分解法外,还有“待定系数”等 4.高中强调多题一解,通性通法。 |